Видео 1. Эксперимент с инерциальным движением шашки в условиях сопротивления среды.

По видео, при помощи программы AVS –редактор (AVS – редактор ver 6.3.3. 235.), составим таблицу.

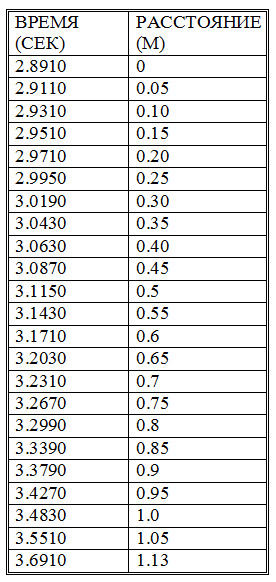
Таблица 1. Экспериментальные данные первого эксперимента инерционного движения шашки.

График экспериментальных данных приведён на рис. 6.

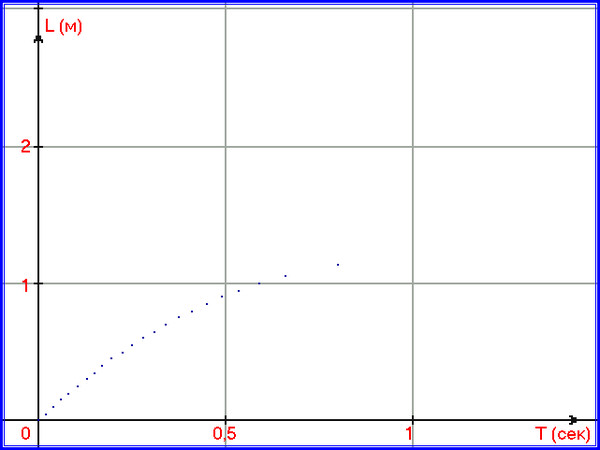
Рис. 6. Экспериментальные данные первого эксперимента инерционного движения шашки.

При построении графика, время было сдвинуто на 2,8910 секунды, поэтому предполагается, что время начала движения совпадает с моментом времени, равном нулю. Такой сдвиг удобен, для изучения явлений в условиях синхронизации.

2.2. Создание математической модели для первого эксперимента инерционного движения шашки. Методика получения модели.

Предположим, что график на рисунке 6 является графиком «экспоненто - разностной» кривой.
Функция экспоненто-разностной кривой получается при вычислении разности экспоненциальной функции

Последняя точка экспериментальных данных не берётся в расчёт, так, как эта точка является точкой остановки движения. Точка остановки движения не принадлежит к функции движения. Это своеобразный сбой движения.
На рис. 7. приведён результат работы по поиску экспоненто-разностной функции.







Рис. 10. Математическая модель для скорости инерциального движения шашки (опыт 1) построена точками зелёного цвета. Экспериментальные данные скорости построены поверх точек математической модели построены точками красного цвета.

Приведённые здесь графики (рис. 6 – рис. 10) и уравнения (1.01), (1.02) представляют собой метод, с помощью которого можно получить модели для инерционного движения тела. К таким моделям относятся: математическая модель пути (1.01) и математическая модель скорости (1.02). Математическая модель скорости может быть названа кривой торможения.
Параметр k, приведённый в (1.02) называется постоянной времени и имеет вид:

В дальнейшем, для того, чтобы не загромождать статью подробностями, я не буду излагать весь метод получения математической модели. Я приведу уже полученные математические модели, вместе с экспериментальными данными, для различных типов инерциального движения в условиях сопротивления среды.

3. Второй опыт с инерционным движением шашки. Изменение импульса броска шашки.

Изменим условия броска шашки, увеличим её начальный импульс, чтобы шашка прошла немного большее расстояние.
Выполним всю работу, которая описана в главе 2. Получим математическую модель инерционного движения шашки.

Видео 2. Второй эксперимент с инерциальным движением шашки в условиях сопротивления среды.
Экспериментальные данные приведены в таблице 2.

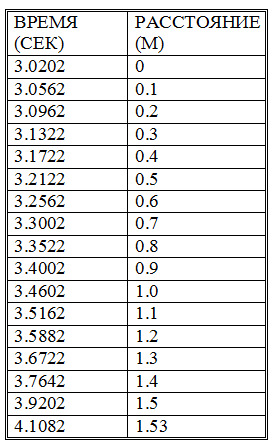
Таблица 2. Экспериментальные данные второго эксперимента инерционного движения шашки.

Математическая модель пути для второго опыта с инерционным движением шашки выглядит так:




Рис. 12. Математическая модель, согласно уравнения (1.05) инерциального движения шашки: опыт 1 и опыт 2. Экспериментальные данные построены поверх точек математической модели. Математическая модель и прямая предельного расстояния для первого опыта построена зелёными точками. Математическая модель и прямая предельного расстояния для второго опыта построена сереневыми точками.
На рисунке 12 приведены две математические модели согласно уравнению:




4. Опыт с инерциальным движением стеклянного шара по горизонтальному деревянному желобу –треку.

Можно было бы поставить опыт с движением шара на плоскости. Но сначала поставим опыт с движением шара в горизонтальном желобе – треке. Такой опыт упрощает задачу привязки движения шара к шкале расстояния. В качестве трека используется деревянный плинтус.
В опыте стеклянному шару рукой придаём импульс, после чего шар движется по желобу – треку до полной остановки. Движение шара записываем видеокамерой с частотой 300 кадров в секунду. Технология проведения опыта и создания математической модели точно такая же, как и для шашки.
Стеклянный шар имеет вес 155 грамм. Диаметр шара 49 мм.

Рис. 13. Стеклянный шар на весах.

Видео 3. Эксперимент с инерциальным движением стеклянного шара в условиях сопротивления среды.

Экспериментальные данные приведены в таблице 3.

Таблица 3. Экспериментальные данные инерционного движения стеклянного шара.





5. Опыт с инерциальным движением по плоскости детского автомобиля с встроенным инерциальным двигателем, на основе маховика.

В опыте автомобилю рукой придаём запас движения, после чего автомобиль движется по плоскости до полной остановки. Движение автомобиля фиксируем видеосъёмкой с частотой 300 кадров в секунду. Технология проведения опыта и создания математической модели точно такая же, как и для шашки.

Рис. 16. Игрушечный детский автомобиль с инерционным двигателем на основе маховика.

Рис. 17. Вид инерционного двигателя на основе маховика.

Видео 4. Эксперимент с инерциальным движением игрушечного автомобиля в условиях сопротивления среды.

Экспериментальные данные приведены в таблице 4.

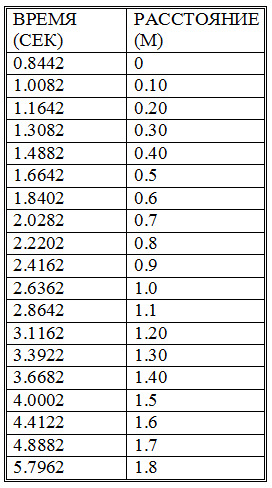
Таблица 4. Экспериментальные данные инерционного движения игрушечного автомобиля.




Современная физика не представляет никакой информации об уравнении движения по инерции в условии сопротивления движению.
Между тем Кориолис написал книгу о бильярде, в которой также не сдвинулся с мёртвой точки.
В чём же основная ошибка современных физических воззрений?

6. Уравнение инерциального движения тела в условиях сопротивления движению.


Рис. 20. Механическая иерархия энергий.

Инерционное движение в условиях сопротивления - это движение, когда скорость уменьшается во времени. Современная физика для такого случая предлагает силу трения. Но такой силы не существует. В данной работе предлагается другой вариант решения . На тело действует в течение всего движения - сила инерции. Её природа следующая - в вакууме эфир увлекает тело.
Почему происходит остановка движения тела при инерционном движении? Какие процессы сохранения энергий происходят при остановке движения тела? Это вопросы, на которые надо искать ответы.
В дальнейшем, попробуем найти другую математическую модель, описывающую инерционное движение. Она должна:
- быть более точной;
- содержать правильные, верные физические параметры;
- обосновывать точку остановки движения.
Для этого продолжим ставить опыты с исследованием инерционного движения.