Leonid Orydoroga,
13-11-2014 17:01
(ссылка)
13 Ведьм на Шабаше.
Эту задачу следовало выложить на Хэллоуин. Но тогда я о ней просто забыл. Вспомнил только сегодня. Думаю, что 13-е число — достаточный повод для её публикации .
В полночь на круглосуточный шабаш слетелось 13 ведьм. Некоторые из этих ведьм знакомы* друг с другом, некоторые — нет.
Те ведьмы, у которых среди шабашниц не было ни одной знакомой, сразу улетели.
В час ночи улетели те, у которых на этот момент на шабаше оставалась ровно 1 знакомая ведьма;
В 2:00 улетели те, у которых на этот момент на шабаше оставались ровно 2 знакомые ведьмы;
В 3:00 улетели те, у которых на этот момент на шабаше оставались ровно 3 знакомые ведьмы;
В 4:00 улетели те, у которых на этот момент на шабаше оставались ровно 4 знакомые ведьмы;
В 5:00 улетели те, у которых на этот момент на шабаше оставались ровно 5 знакомых ведьм;
В 6:00 улетели те, у которых на этот момент на шабаше оставались ровно 6 знакомых ведьм;
В 7:00 улетели те, у которых на этот момент на шабаше оставались ровно 7 знакомых ведьм;
В 8:00 улетели те, у которых на этот момент на шабаше оставались ровно 8 знакомых ведьм;
В 9:00 улетели те, у которых на этот момент на шабаше оставались ровно 9 знакомых ведьм;
В 10:00 улетели те, у которых на этот момент на шабаше оставались ровно 10 знакомых ведьм;
В 11:00 улетели те, у которых на этот момент на шабаше оставались ровно 11 знакомых ведьм;
Наконец, в полдень улетели те, у которых на этот момент на шабаше оставались ровно 12 знакомых ведьм.
Оставшиеся после этого ведьмы шабашили ещё 12 часов, до следующей полуночи.
Какое наибольшее число ведьм могло оставаться на шабаше в 13:00?
* Знакомство симметрично (если ведьма А знакома с ведьмой В, то и ведьма В знакома с ведьмой А); антирефлексивно (ни одна ведьма не знакома сама с собой); не транзитивно (если ведьма А знакома с ведьмой В и ведьма В знакома с ведьмой С, то отсюда не следует, что ведьма А знакома с ведьмой С).
Метки: Хиппи, 13 Число, Комбинаторика, Графы
Leonid Orydoroga,
13-11-2014 01:02
(ссылка)
Игра. (Тринадцатое, Четверг.)
Два игрока по-очереди выставляют ладей на доску 4х13.
Сначала доска пустая.
Первому игроку разрешается ставить ладью на пустую клетку, атакованную чётным числом ладей; второму — на пустую клетку, атакованную нечётным числом ладей. Проигрывает игрок, который не может сделать очередной ход.
Кто выиграет при правильной игре? Укажите выигрышную стратегию.
(Ладьи не рентгеновские! Например, если ладьи стоят на полях а1, а2, а3 то поле а4 атакует только одна ладья — а3.)
Метки: Хиппи, 13 число, комбинаторика, Игра, Выигрышная Стратегия, Клетчатая Доска, Олимпиадная Задача
Евгения Костина,
12-11-2014 12:46
(ссылка)
теория вероятности
подскажите, умные люди!!
Из трех групп спортсменов выбирают на соревнования !В 1 группе норматив выполнили 20%,во 2=40%,в 3=70%
Наугад выбирают одного спортсмена .какова вероятность , что он оказался из 3 группы)
Из трех групп спортсменов выбирают на соревнования !В 1 группе норматив выполнили 20%,во 2=40%,в 3=70%
Наугад выбирают одного спортсмена .какова вероятность , что он оказался из 3 группы)
Червяков Сергей,
11-11-2014 00:06
(ссылка)
Уравнение
Ещё одна задача Творческого конкурса учителей математики (сентябрь 2014).
Уравнение. Докажите, что при всех натуральных n уравнение
1 + 2x + 3x² + 4x³ + … + n*x^(n−1) = n²
имеет хотя бы один рациональный корень, принадлежащий интервалу (1; 2).
Уравнение. Докажите, что при всех натуральных n уравнение
1 + 2x + 3x² + 4x³ + … + n*x^(n−1) = n²
имеет хотя бы один рациональный корень, принадлежащий интервалу (1; 2).
Метки: Творческий конкурс
Червяков Сергей,
11-11-2014 00:03
(ссылка)
Прямые
Ещё одна из задач Творческого конкурса учителей математики (сентябрь 2014)
Прямые. Даны две скрещивающиеся прямые. Все прямые, которые пересекают обе
данные, красят в синий цвет. Укажите все точки пространства, которые останутся
неокрашенными.
Прямые. Даны две скрещивающиеся прямые. Все прямые, которые пересекают обе
данные, красят в синий цвет. Укажите все точки пространства, которые останутся
неокрашенными.
Червяков Сергей,
10-11-2014 23:58
(ссылка)
Квадраты
Задачи из Творческого конкурса учителей математики (сентябрь 2014).
Квадраты. Из клетчатой бумаги по линиям сетки вырезали большой квадрат. Из него,
также по линиям сетки, вырезали меньший квадрат. После этого от большого квадрата
осталось ровно 79 клеток. Обязательно ли вырезанный квадрат содержал одну из
угловых клеток большого?
Квадраты. Из клетчатой бумаги по линиям сетки вырезали большой квадрат. Из него,
также по линиям сетки, вырезали меньший квадрат. После этого от большого квадрата
осталось ровно 79 клеток. Обязательно ли вырезанный квадрат содержал одну из
угловых клеток большого?
Leonid Orydoroga,
08-11-2014 14:32
(ссылка)
Нечётный прямоугольник.
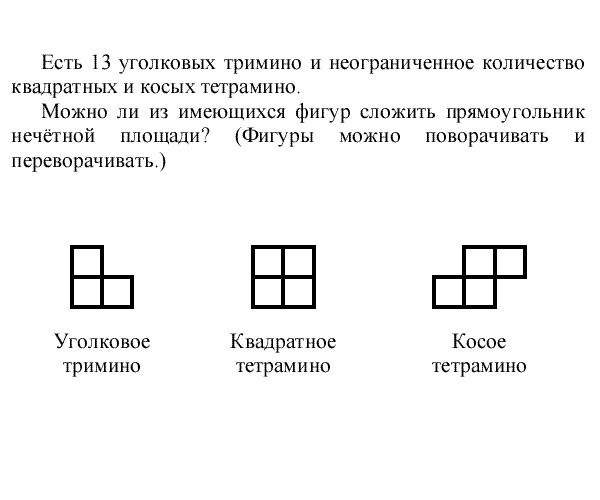
Метки: Хиппи, комбинаторика, Олимпиадная Задача, Головоломка, Клетчатая Доска, разрезания, Полимино
Евгения Костина,
17-10-2014 02:16
(ссылка)
дифференциальное исчисление
Закон движения материальной точки задается уравнениями : х=mt +6; y=nt
Наити ее скорость и вычислить координаты через 10 секунд
Дополнен 1 минуту назад
если значения m=7? n=29
как наити производную???? Скорость - это производная от пути по времени
как ее наити и вычислить координаты
Наити ее скорость и вычислить координаты через 10 секунд
Дополнен 1 минуту назад
если значения m=7? n=29
как наити производную???? Скорость - это производная от пути по времени
как ее наити и вычислить координаты
Евгений Фёдоров,
11-09-2014 21:25
(ссылка)
Еще уравнение
x² + {x}x + [x] = 0
где {x}, [x] - дробная и целая части х.
где {x}, [x] - дробная и целая части х.
Евгений Фёдоров,
30-08-2014 11:49
(ссылка)
Мошенники и жулики!
Внимание! Мошенники и жулики!
Сайт http://olympiads.biz/ - платная подготовка к олимпиадам.
Своровали беспардонно и выложили без какого-либо моего разрешения, без ссылки на автора, трусливо, анонимно мои решения олимпиадных задач и рисунки. Опубликовали их под ником "kovalev".
Я на этом сайте не смог зарегистрироваться, чтобы выяснить ситуацию - скорее всего заблокировали.
Предостерегаю - НЕ доверяйте ВОРАМ, мошенникам и проходимцам!
Эти бездари даже воровать не умеют, тем более не смогут подготовить к олимпиадам по математике.
Сайт http://olympiads.biz/ - платная подготовка к олимпиадам.
Своровали беспардонно и выложили без какого-либо моего разрешения, без ссылки на автора, трусливо, анонимно мои решения олимпиадных задач и рисунки. Опубликовали их под ником "kovalev".
Я на этом сайте не смог зарегистрироваться, чтобы выяснить ситуацию - скорее всего заблокировали.
Предостерегаю - НЕ доверяйте ВОРАМ, мошенникам и проходимцам!
Эти бездари даже воровать не умеют, тем более не смогут подготовить к олимпиадам по математике.
Евгений Фёдоров,
21-07-2014 21:01
(ссылка)
ЕГЭ - В10
Интересно, как Вы думаете, это задача уровня В?
Какой ответ в этой задаче?

Евгений Фёдоров,
27-04-2014 23:55
(ссылка)
Акция на распродаже.
Магазин проводит акцию по продаже теннисных мячей.
Каждый, кто покупает набор из трех пакетов мячей такой, что
во втором пакете в 2 раза больше мячей, чем в первом пакете,
в третьем пакете в 3 раза больше мячей, чем в первом пакете,
может бесплатно взять еще один набор из трех пакетов, с таким же числом мячей в каждом пакете. Один мячик стоит 5 рублей.
Как много мячей можно купить на 30 рублей?
Каждый, кто покупает набор из трех пакетов мячей такой, что
во втором пакете в 2 раза больше мячей, чем в первом пакете,
в третьем пакете в 3 раза больше мячей, чем в первом пакете,
может бесплатно взять еще один набор из трех пакетов, с таким же числом мячей в каждом пакете. Один мячик стоит 5 рублей.
Как много мячей можно купить на 30 рублей?
Метки: Арифметика
Червяков Сергей,
26-04-2014 14:28
(ссылка)
Оптимальная стратегия
Вася и Петя закрашивают по очереди клетки на доске размером 4×4 так, чтобы не образовывался квадрат 2×2 из закрашенных клеток. Тот, кто не сможет сделать очередной ход, проигрывает. Начинает Петя. Кто из них сможет выиграть, как бы ни играл соперник?
Червяков Сергей,
26-04-2014 14:22
(ссылка)
Равнобедренный треугольник
И ещё одна задача.
В равнобедренном треугольнике АВС (АВ = АС) провели биссектрису BD. Оказалось, что ВС = BD + AD. Найдите угол BАC.
В равнобедренном треугольнике АВС (АВ = АС) провели биссектрису BD. Оказалось, что ВС = BD + AD. Найдите угол BАC.
Червяков Сергей,
26-04-2014 14:21
(ссылка)
Указ о гуманизауии образования
Продолжаю публиковать задачи из VII заочного конкурса учителей матемватики.
У Мудрого Учителя Фу есть любимый Ученик Ли. Каждый день Фу вкладывает знания в Ли. Однажды Фу обнаружил, что Ли усваивает на занятии не весь вложенный объем знаний, а только логарифм этого объема (например, если Фу вкладывает в Ли единицу знаний, то Ли не усваивает ничего). Основание логарифма – величина, обратная длине палки (в метрах), с помощью которой Фу вкладывает знания в Ли. Однажды Император издал указ о гуманизации образования, в котором повелел укоротить все палки. До какой наименьшей длины Фу может укоротить палку, чтобы ею можно было вложить в Ли столько знаний, что Ли их усвоит без остатка?
У Мудрого Учителя Фу есть любимый Ученик Ли. Каждый день Фу вкладывает знания в Ли. Однажды Фу обнаружил, что Ли усваивает на занятии не весь вложенный объем знаний, а только логарифм этого объема (например, если Фу вкладывает в Ли единицу знаний, то Ли не усваивает ничего). Основание логарифма – величина, обратная длине палки (в метрах), с помощью которой Фу вкладывает знания в Ли. Однажды Император издал указ о гуманизации образования, в котором повелел укоротить все палки. До какой наименьшей длины Фу может укоротить палку, чтобы ею можно было вложить в Ли столько знаний, что Ли их усвоит без остатка?
Червяков Сергей,
26-04-2014 14:18
(ссылка)
Найти неисправные весы
У завхоза было трое одинаковых чашечных весов. В одних потерялась часть деталей, и теперь они могут показывать что угодно. Любые весы помещаются на одну чашку других весов. За какое наименьшее количество взвешиваний можно определить неисправные весы?
Евгений Фёдоров,
18-04-2014 15:05
(ссылка)
Сколько дней продлится водопой?
В сезон дождей котлован в африканском заповеднике заполняется водой. Затем, в солнечные безоблачные дни вода из котлована равномерно испаряется. Наконец, когда её не остается вовсе, наступает засуха. И так каждый год.
Когда заканчиваются дожди, к котловану ходят утолять жажду слоны и буйволы. Приходят каждый день, пока есть вода.
В первый год 50 слонов и 70 буйволов выпили воду за 60 дней.
Во второй год 40 слонов и 60 буйволов утоляли жажду 72 дня.
В третий год 30 слонов и 40 буйволов ходили на водопой 100 дней.
В этом году в заповеднике 24 слона и 34 буйвола.
Сколько дней продлится водопой?
Метки: Арифметика
Евгений Фёдоров,
04-04-2014 19:21
(ссылка)
Задача для 5-го класса.
Позвонила знакомая, её дочка учится в 5-м классе.
Учительница задала им такую задачу.
Из пунктов А и В одновременно навстречу друг другу выехали автомобиль и мотоцикл. Через час автомобиль был посередине между пунктом А и мотоциклом. Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.
Найти отношение скоростей мотоцикла и автомобиля.
По-моему, для 5-го класса это слишком.
Дал эту задачу на одном форуме, никто пока не решил.
Учительница задала им такую задачу.
Из пунктов А и В одновременно навстречу друг другу выехали автомобиль и мотоцикл. Через час автомобиль был посередине между пунктом А и мотоциклом. Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.
Найти отношение скоростей мотоцикла и автомобиля.
По-моему, для 5-го класса это слишком.
Дал эту задачу на одном форуме, никто пока не решил.
Метки: Арифметика
Евгений Фёдоров,
06-02-2014 15:56
(ссылка)
Взвешивание.
Имеется 16 коробок с монетами. В каждой коробке монеты одного веса и металла.
4 коробки с золотыми монетами весом 1, 2, 3 и 4 грамма.
4 коробки с серебряными монетами весом 1, 2, 3 и 4 грамма.
8 коробок с медными монетами весом 1, 2, ..., 7 и 8 граммов.
В одной из коробок все монеты фальшивые.
Можно ли за 4 взвешивания на чашечных весах определить коробку с фальшивыми монетами и узнать легче они или тяжелее?
Евгений Фёдоров,
14-01-2014 17:39
(ссылка)
С Новым Годом!
Решить уравнение
2014 + 2arctg x + arcsin(2x/(1 + x^2)) = x^2.
Leonid Orydoroga,
13-12-2013 21:21
(ссылка)
N гирь (снова пятница 13-е).
N — натуральное число. Известно, что сумма остатков от деления N на 3, 8, 135 и 2013 равна 1313.
Можно ли набор из гирь весом 1, 2, 3, 4, … , N разложить на две кучки равной массы?
Метки: 13 число, Хиппи, математика, Арифметика, комбинаторика
задача
Задача. Внутри квадрата со стороной 10 отметили 6 различных точек, все попарные расстояния между которыми – целые числа. Доказать, что среди этих расстояний найдутся равные.
Евгения Костина,
08-11-2013 02:00
(ссылка)
круги Эйлера
в классе 12 человек любят щи ,14 любят суп,12 любят борщ,из них 2 человека любят щи и суп,4 брщ и суп,3 щи и борщ,а 3 человека любят все три блюда.сколько человек в классе,если нет не одного не любящего супы.
Белый и Пушистый,
16-10-2013 10:26
(ссылка)
как доказать делимость на 11 ?
доказать делимость на 11
выражения 8*(3^(5*k)+5^(5*n))-5, где n и k - натуральные
выражения 8*(3^(5*k)+5^(5*n))-5, где n и k - натуральные
В этой группе, возможно, есть записи, доступные только её участникам.
Чтобы их читать, Вам нужно вступить в группу
Чтобы их читать, Вам нужно вступить в группу
