Leonid Orydoroga,
13-10-2013 21:33
(ссылка)
Купюры в конвертах.
Сколькими способами можно разложить 13 различных купюр по 5 одинаковым конвертам?
(Некоторые конверты могут остаться пустыми. Например, один из способов — положить все 13 купюр в один конверт.)
Метки: Хиппи, 13 число, комбинаторика, математика
Евгения Костина,
03-10-2013 14:25
(ссылка)
Без заголовка
в соревнованиях 58%
участников получили подарки. Довольными итогами конкурса остались 95%
участников,причём 60% из них получили подарков.Какая часть недовольных результатами конкурса участников получила призы?
участников получили подарки. Довольными итогами конкурса остались 95%
участников,причём 60% из них получили подарков.Какая часть недовольных результатами конкурса участников получила призы?
Евгений Фёдоров,
28-09-2013 18:24
(ссылка)
А паук все ползет и ползет.
Наум Коржавин.
Вариации из Некрасова
"...
Ей жить бы хотелось иначе,
Носить драгоценный наряд...
Но кони - всё скачут и скачут.
А избы - горят и горят."
Вариации старинной задачи
На поверхности прямоугольного параллелепипеда размером 4 х 6 х 12 взята точка А.
Какая точка наиболее удаленная по поверхности от точки А (паук ползет по поверхности), если
1) А вершина параллелепипеда?
2) А центр грани 6 х 12?
3) А центр грани 4 х 12?
4) А центр грани 4 х 6?
Проводом какой минимальной длины можно соединить (протягивая провод по поверхности) две любые точки поверхности параллелепипеда?
Вариации из Некрасова
"...
Ей жить бы хотелось иначе,
Носить драгоценный наряд...
Но кони - всё скачут и скачут.
А избы - горят и горят."
Вариации старинной задачи
На поверхности прямоугольного параллелепипеда размером 4 х 6 х 12 взята точка А.
Какая точка наиболее удаленная по поверхности от точки А (паук ползет по поверхности), если
1) А вершина параллелепипеда?
2) А центр грани 6 х 12?
3) А центр грани 4 х 12?
4) А центр грани 4 х 6?
Проводом какой минимальной длины можно соединить (протягивая провод по поверхности) две любые точки поверхности параллелепипеда?
Метки: Занимателная арифметика
Leonid Orydoroga,
24-09-2013 14:06
(ссылка)
Поиск закономерностей.
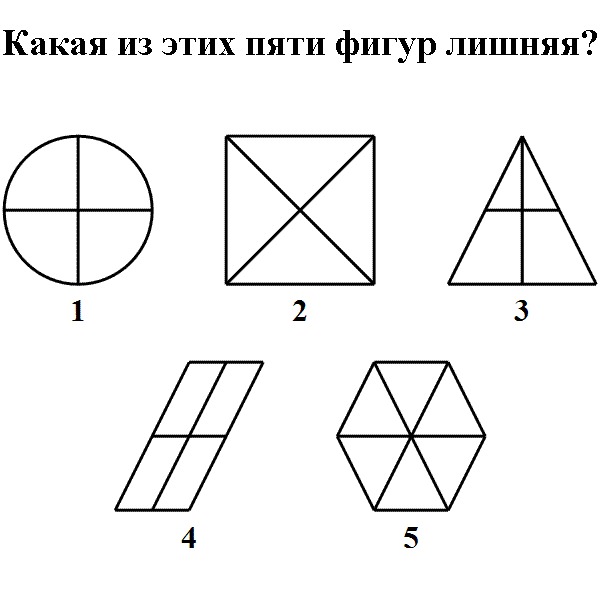
Метки: Хиппи, Головоломка, загадка, IQ, тест
Leonid Orydoroga,
13-09-2013 12:04
(ссылка)
Сумма цифр. (Снова пятница 13-е.)
а) Целое положительное число умножили на 13. Может ли сумма цифр произведения быть в 5 раз меньше суммы цифр исходного числа?
б) Целое положительное число умножили на 5. Может ли сумма цифр произведения быть в 13 раз меньше суммы цифр исходного числа?
Метки: Хиппи, 13 число, Целые числа, Арифметика, Олимпиадная Задача
Leonid Orydoroga,
13-08-2013 20:47
(ссылка)
Четырнадцатирукий Бог у входа в монастырь.
Метки: Хиппи, 13 число, стереометрия, комбинаторика, олимпиада
Екатерина Н.,
10-08-2013 21:09
(ссылка)
Задача на построение
На плоскости даны две точки А и В. Интересно, как одним только циркулем построить середину отрезка АВ ?
Метки: задача, построения, геометрия
Екатерина Н.,
09-08-2013 22:53
(ссылка)
Просто интересно...
Интересно: существует ли такое натуральное число, которое заканчивается на 2012 и кратное 2013 ?
Евгений Фёдоров,
25-07-2013 21:28
(ссылка)
Во сколько раз дороже?
КУБ размером 3 х 3 х 3 составлен из набора кубиков размером 1 х 1 х 1, каждая грань которых окрашена либо золотой, либо серебряной краской.
Для одного и того же набора возможна такая расстановка кубиков, при которой все грани КУБа будут золотые, ровно как и возможна расстановка, при которой все грани КУБа - серебряные.
Окраска грани кубика серебряной краской стоит 3 монеты, золотой - 11 монет.
Во сколько раз самый дорогой КУБ дороже самого дешевого?
Для одного и того же набора возможна такая расстановка кубиков, при которой все грани КУБа будут золотые, ровно как и возможна расстановка, при которой все грани КУБа - серебряные.
Окраска грани кубика серебряной краской стоит 3 монеты, золотой - 11 монет.
Во сколько раз самый дорогой КУБ дороже самого дешевого?
Метки: занимательная задача
Евгений Фёдоров,
25-07-2013 11:26
(ссылка)
Мех-мат 2013. Задача №8.
Найти все значения параметра а, при которых уравнение
cos(x + a/x) = x - 1
имеет бесконечное число решений.
cos(x + a/x) = x - 1
имеет бесконечное число решений.
Метки: параметр
Продолжение одной старой задачки
Даны окружность ω с центром O и касающаяся её в точке A прямая l.
1. (Старая задачка.) Найти геометрическое место центров окружностей, касающихся l и ω. (Ответ: парабола с вершиной A и фокусом O.)
2. (Продолжение.) Пусть B — точка на окружности ω, диаметрально противоположная A. Рассмотрим произвольную окружность, касающуюся l и ω, и проведём к ней из точки B касательные. Найти геометрическое место точек касания.
1. (Старая задачка.) Найти геометрическое место центров окружностей, касающихся l и ω. (Ответ: парабола с вершиной A и фокусом O.)
2. (Продолжение.) Пусть B — точка на окружности ω, диаметрально противоположная A. Рассмотрим произвольную окружность, касающуюся l и ω, и проведём к ней из точки B касательные. Найти геометрическое место точек касания.
Метки: геометрия
Leonid Orydoroga,
13-07-2013 17:41
(ссылка)
Суперигра в телешоу "Страна Дураков".
Суперигра в телешоу "Страна Дураков" проходит следующим образом:
В студию выносят 2013 шкатулок, пронумерованных числами от 1 до 2013.
В одной из шкатулок лежит приз. Ведущий телешоу, Тышарович, точно знает в какой именно.
Игрок пишет 13 записок. В каждой из записок — 1 вопрос, на который можно однозначно ответить либо "Да" либо "Нет".
Тышарович, прочитав записки, две из них откладывает в сторону, а на остальные 11 последовательно отвечает (по одному разу на каждую). При этом Игрок не знает, ни на какие вопросы ответил Ведущий, ни в каком порядке.
После этого Игрок называет номер шкатулки. Её открывают и Игрок получает содержимое.
Игрок заинтересован в том, чтобы получить приз. Ведуший — в том, чтобы Игрок не угадал номер призовой шкатулки.
Какую максимальную вероятность выигрыша может гарантировать себе Игрок?
(Предполагается, что и Игрок и Ведущий могут производить в уме как угодно сложные вычисления.)
Метки: Хиппи, 13 число, вероятность, игра
Leonid Orydoroga,
13-07-2013 16:52
(ссылка)
Равнобедренный треугольник.
ABC — равнобедренный треугольник (AC=BC).
Биссектриса угла A равна удвоенной биссектрисе угла C.
Доказать, что центры вписанной и описанной окружностей треугольника ABC симметричны относительно стороны AB.
Leonid Orydoroga,
13-07-2013 16:37
(ссылка)
Красим квадрат.
Клетки квадрата размером 2013Х2013 клеток раскрашены в n цветов. Из него вырезают квадратик 13Х13 клеток. Известно, что независимо от того, в каком месте вырезается квадратик, в нём обязательно найдётся ровно одна нецентральная клетка, окрашенная в тот же цвет, что и центральная.
При каком наименьшем n это возможно?
Метки: Хиппи, 13 число, Олимпиадная Задача, комбинаторика, раскраски, Клетчатая Доска
Leonid Orydoroga,
13-04-2013 08:25
(ссылка)
Что больше? (13/4/2013)
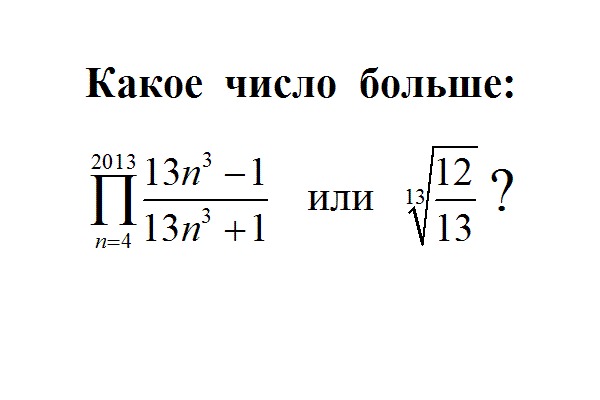
Метки: Хиппи, 13 число, Олимпиадная Задача, анализ
Евгения Костина,
03-04-2013 20:24
(ссылка)
решить
Найдите расстояние между
точками а и в если а(3,9-x) ,b (-x-1,5)
точками а и в если а(3,9-x) ,b (-x-1,5)
Leonid Orydoroga,
01-04-2013 20:35
(ссылка)
Первоапрельская задача #2.
По условию задачи придумайте, что в ней спрашивается.
1 апреля 2012 года профессор написал на доске числа 1 и 2. После этого ассистент каждый день стирает написанные числа и пишет вместо них их среднее арифметическое и среднее гармоническое. (Таким образом 2 апреля на доске будет написано 3/2 и 4/3; 3 апреля 17/12 и 24/17; и т.д.)
Так он поступает до сегодня (т.е. до 1 апреля 2013 года).
Поздравляю всех с 1 апреля!
Метки: Хиппи, 1 апреля, придумайте сами
Leonid Orydoroga,
01-04-2013 20:35
(ссылка)
Первоапрельская задача #1.
Первый покупатель: Мне 4.
Продавец: с Вас 20.
Второй покупатель: Мне 32.
Продавец: с Вас 40.
Третий покупатель: Мне 256.
Продавец: с Вас 60.
Четвёртый покупатель: Мне 2048.
Продавец: с Вас 80.
Что они покупали?
Поздравляю всех с 1 апреля!
Метки: Хиппи, 1 апреля, Прогрессия
Leonid Orydoroga,
13-03-2013 13:30
(ссылка)
Уравнение с параметром.
Метки: Хиппи, 13 число, Олимпиадная Задача, уравнение, параметр
Leonid Orydoroga,
11-03-2013 16:18
(ссылка)
Треугольник.
Навеяно задачей, которую сегодня увидел в интернете.
О треугольнике ABC известно, что на прямой BC нет точки K, отличной от точки B, такой, что |AK|*|BC| = |AB|*|CK|, но есть точка L, отличная от точки C, такая, что |AL|*|BC| = |AC|*|BL|.
Доказать, что треугольник равнобедренный.
PS В вопрос о 8 марта внесено изменение.
8 марта этого года связано даже с ПЯТЬЮ последовательными элементами хорошо известной последовательности.
Метки: Хиппи, Олимпиадная Задача, геометрия
Leonid Orydoroga,
08-03-2013 22:54
(ссылка)
С 8 Марта, Дорогие Сообщницы!!!
Сегодня я обнаружил, что сегодняшняя дата напрямую связана с пятью последовательными числами из хорошо известной последовательности. Назовите эти 5 чисел и укажите связь.
Милые участницы сообщества!
Поздравляю с 8 Марта!!!
Поздравляю с 8 Марта!!!
хочется: Всех поздравить с 8 Марта!!!
В этой группе, возможно, есть записи, доступные только её участникам.
Чтобы их читать, Вам нужно вступить в группу
Чтобы их читать, Вам нужно вступить в группу
